Nonlinear oscillator

This example implements a nonlinear harmonic oscillator in a 2D neural population. Unlike the simple oscillator whose recurrent connection implements a linear transformation, this model approximates a nonlinear function in the recurrent connection to yield oscillatory behavior.

import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np

import nengo
import nengo_loihi
nengo_loihi.set_defaults()

/home/travis/build/nengo/nengo-loihi/nengo_loihi/version.py:23: UserWarning: This version of `nengo_loihi` has not been tested with your `nengo` version (3.0.1.dev0). The latest fully supported version is 3.0.0
  "supported version is %s" % (nengo.__version__, latest_nengo_version)
/home/travis/virtualenv/python3.6.3/lib/python3.6/site-packages/nengo_dl/version.py:42: UserWarning: This version of `nengo_dl` has not been tested with your `nengo` version (3.0.1.dev0). The latest fully supported version is 3.0.0.
  % ((nengo.version.version,) + latest_nengo_version)

Creating the network in Nengo

Our model consists of one recurrently connected ensemble. Unlike the simple oscillator, we do not need to give this nonlinear oscillator an initial kick.

tau = 0.1


def recurrent_func(x):
    x0, x1 = x
    r = np.sqrt(x0**2 + x1**2)
    a = np.arctan2(x1, x0)
    dr = -(r - 1)
    da = 3.0
    r = r + tau*dr
    a = a + tau*da
    return [r*np.cos(a), r*np.sin(a)]


with nengo.Network(label='Oscillator') as model:
    ens = nengo.Ensemble(200, dimensions=2)
    nengo.Connection(ens, ens,
                     function=recurrent_func,
                     synapse=tau)
    ens_probe = nengo.Probe(ens, synapse=0.1)

Running the network in Nengo

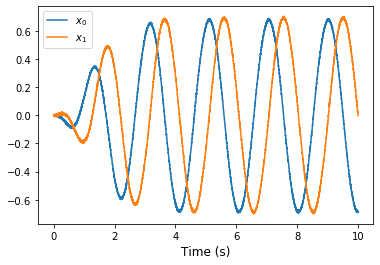
We can use Nengo to see the desired model output.

with nengo.Simulator(model) as sim:
    sim.run(10)
t = sim.trange()

0%

 

0%

 

def plot_over_time(t, data):
    plt.figure()
    plt.plot(t, data[ens_probe])
    plt.xlabel('Time (s)', fontsize='large')
    plt.legend(['$x_0$', '$x_1$'])


plot_over_time(t, sim.data)

def plot_xy(data):
    plt.figure()
    plt.plot(data[ens_probe][:, 0], data[ens_probe][:, 1])
    plt.xlabel('$x_0$', fontsize='x-large')
    plt.ylabel('$x_1$', fontsize='x-large')


plot_xy(sim.data)

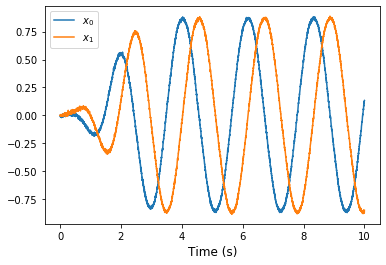
Running the network with Nengo Loihi

with nengo_loihi.Simulator(model) as sim:
    sim.run(10)
t = sim.trange()

/home/travis/build/nengo/nengo-loihi/nengo_loihi/discretize.py:471: UserWarning: Lost 2 extra bits in weight rounding
  warnings.warn("Lost %d extra bits in weight rounding" % (-s2,))

plot_over_time(t, sim.data)

plot_xy(sim.data)